Was ist logistische Regression?
Einführung in die logistische Regression
Die logistische Regression ist eine grundlegende Methode im maschinellen Lernen und in der prädiktiven Analyse, die verwendet wird, um die Wahrscheinlichkeit eines Ergebnisses basierend auf definierten Variablen zu schätzen. Sie verwandelt komplexe Daten in klare Erkenntnisse und hilft Organisationen, informierte, datengestützte Entscheidungen zu treffen.
In ihrer einfachsten Form ist die logistische Regression ein statistisches Modell, das die Wahrscheinlichkeit eines Ereignisses schätzt, indem es die Beziehungen zwischen erklärenden Variablen und einer abhängigen Variablen analysiert. Die Ergebnisse werden als Quoten ausgedrückt, die dann mit der logistischen (sigmoid) Funktion in Wahrscheinlichkeiten umgewandelt werden.
Diese Seite erklärt, wie die logistische Regression funktioniert, warum sie wichtig ist und wie sie skalierbare prädiktive Analysen, KI und überwachtes Lernen in modernen Cloud-Computing-Umgebungen unterstützt.
Definition und Zweck
Die logistische Regression sagt die Wahrscheinlichkeit eines kategorialen Ergebnisses voraus, normalerweise binär, wie Erfolg/Misserfolg oder Ja/Nein. Sie schätzt die Beziehung zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen und produziert Ergebnisse, die als Quoten oder Wahrscheinlichkeitswerte interpretiert werden können.
Im Gegensatz zur linearen Regression, die kontinuierliche Werte vorhersagt, führt die logistische Regression eine Klassifikation durch und bestimmt, ob eine Beobachtung zu einer Klasse oder einer anderen gehört – zum Beispiel ‚Spam‘ vs ‚kein Spam‘ oder ‚genehmigt‘ vs ‚abgelehnt‘.
Da sie einfach, aber leistungsstark ist, bleibt die logistische Regression eines der am häufigsten verwendeten Modelle in der KI, Cloud-Analytik und Datenplattformen, die große Datensätze für überwachte Lernprozesse verarbeiten. Ihre Transparenz und Interpretierbarkeit machen sie ideal, um zu verstehen, wie jedes Merkmal ein bestimmtes Ergebnis beeinflusst, sei es die Vorhersage des Krankheitsrisikos, der Kundenabwanderung oder der Systemzuverlässigkeit.
Wenn sie auf öffentlichen Cloud-Plattformen implementiert wird, unterstützt sie skalierbare prädiktive Analysen und robuste Datenplattformen. Die Kombination mit Infrastrukturmanagement und zuverlässiger Cloud-Architektur bietet eine sichere, leistungsstarke Basis für alles, von linearen Regressionsmodellen bis hin zu LLM-Trainings.
Wie logistische Regression funktioniert
Die logistische Regression ist ein grundlegendes Modell des maschinellen Lernens und der Statistik, das in prädiktiven Analysen verwendet wird, um die Wahrscheinlichkeit eines Ergebnisses zu schätzen. Sie bewertet, wie verschiedene Variablen die Ergebnisse beeinflussen, und verwandelt komplexe Daten in Wahrscheinlichkeiten zwischen 0 und 1.
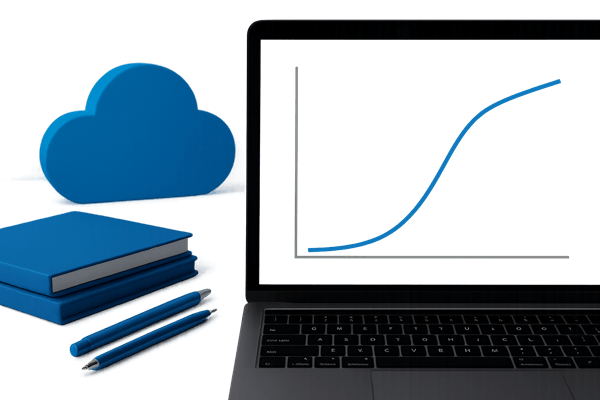
Mit der logistischen (sigmoid) Funktion ordnet sie Eingaben einer S-förmigen Kurve zu und zeigt, wie kleine Änderungen in Faktoren die Wahrscheinlichkeit eines Ereignisses beeinflussen – wie Erfolg vs. Misserfolg. Wenn der interne Wert (Logit) neutral ist, beträgt die Wahrscheinlichkeit 50%; wenn er steigt oder fällt, wird das Ergebnis wahrscheinlicher oder unwahrscheinlicher.
Durch die Optimierung dieser Beziehungen bietet die logistische Regression eine klare, interpretierbare Verbindung zwischen Eingaben und Ergebnissen – sie kombiniert Transparenz und Genauigkeit. Die Koeffizienten zeigen den Einfluss jedes Faktors, und das Odds Ratio quantifiziert deren Auswirkungen, was sie zu einem vertrauenswürdigen Werkzeug in KI, Cloud-Analytik und überwachten Lernprozessen macht.
Bedeutung in der statistischen Analyse
Die logistische Regression spielt eine entscheidende Rolle in der statistischen Analyse und im maschinellen Lernen, da sie traditionelle Statistik und moderne prädiktive Analytik verbindet. Sie ermöglicht Analysten, über einfache Korrelationen hinauszugehen und zu messen, wie erklärende Variablen eine abhängige Variable beeinflussen, während sie klar und interpretierbar bleibt.
Im Gegensatz zu komplexeren oder ‚Black-Box‘-KI- und LLM-Modellen ist die logistische Regression transparent: Jedes Parameter zeigt direkt, wie ein Merkmal die Chancen eines Ergebnisses beeinflusst. Ein positiver Koeffizient erhöht die Wahrscheinlichkeit des Ereignisses, während ein negativer sie verringert.
Diese Klarheit macht die logistische Regression zu einem wesentlichen Modell im überwachten Lernen, das verwendet wird, um Hypothesen zu testen, Risiken zu bewerten und datengestützte Entscheidungen in Bereichen wie Gesundheitswesen, Finanzen und Cloud-Computing zu treffen.
Vergleich mit anderen Regressionsmodellen
Obwohl logistische und lineare Regression mathematische Grundlagen teilen, dienen sie unterschiedlichen Zwecken. Die lineare Regression sagt kontinuierliche Werte voraus, während die logistische Regression Wahrscheinlichkeiten schätzt und Ergebnisse in definierte Kategorien klassifiziert.
Anstatt eine gerade Linie durch Datenpunkte zu legen, verwendet die logistische Regression die Sigmoidfunktion, um Vorhersagen zwischen 0 und 1 abzubilden. Dieser Ansatz minimiert den Verlust durch Likelihood-Schätzung und Gradientenabstieg, was eine zuverlässige Klassifizierung selbst bei binären, multinomialen oder ordinalen Variablen ermöglicht.
In der Praxis bietet die logistische Regression Interpretierbarkeit und Stabilität, während die lineare Regression Präzision für kontinuierliche Vorhersagen bietet, und zusammen bilden sie die Grundlage vieler prädiktiver Modelle, die in maschinellem Lernen und Datenanalyse verwendet werden.
Arten der logistischen Regression
Die logistische Regression kann je nach Anzahl der möglichen Ergebnisse und der Struktur der Daten verschiedene Formen annehmen. Jedes Modell wendet die gleiche logistische Funktion an und versucht, den Verlust zu minimieren, indem es seine Parameter für die beste Anpassung zwischen vorhergesagten und beobachteten Werten anpasst.
- Binäre logistische Regression
Die häufigste Art, die verwendet wird, wenn die abhängige Variable zwei mögliche Ergebnisse hat, zum Beispiel Erfolg/Misserfolg oder Ja/Nein. Sie modelliert den Logarithmus des Chancenverhältnisses, um die Wahrscheinlichkeit einer Klasse vorherzusagen und mehrere erklärende Variablen in einen einzigen Entscheidungspunkt umzuwandeln.
- Multinomiale logistische Regression
Verwendet, wenn das Ergebnis mehr als zwei Kategorien hat. Das Modell vergleicht Logit-Verhältnisse zwischen Klassen, um vorherzusagen, welche Menge von erklärenden Variablen die Daten am besten erklärt. Häufige Anwendungen sind Produktpräferenzen oder Textklassifikation.
- Ordinale logistische Regression
Geeignet, wenn Kategorien eine natürliche Reihenfolge haben, wie z.B. Zufriedenheitsstufen. Es wird angenommen, dass Änderungen in den erklärenden Variablen den Logarithmus des Odds Ratios konsistent über geordnete Punkte verschieben, was es effektiv für rangbasierte Analysen macht.
Über alle Typen hinweg berücksichtigt die logistische Regression zufällige Variationen, interpretiert Verhältnisse klar und verwandelt komplexe Daten in messbare Mittel für genaue Vorhersagen.
Anwendungen der logistischen Regression
Aufgrund ihrer Vielseitigkeit ist die logistische Regression eines der am häufigsten verwendeten Modelle in der Datenanalyse, im maschinellen Lernen und in der prädiktiven Analyse. Sie hilft Organisationen, informierte, datengestützte Entscheidungen zu treffen, indem sie komplexe Daten in messbare Wahrscheinlichkeiten und klare Ergebnisse umwandelt.
Im Wesentlichen unterstützt die logistische Regression die Entscheidungsfindung, wo immer Wahrscheinlichkeit von Bedeutung ist, von der Klassifizierung von Ergebnissen und der Risikobewertung bis hin zur Erkennung von Anomalien und der Vorhersage des Nutzerverhaltens. Ihre Interpretierbarkeit und mathematische Einfachheit machen sie zu einem vertrauenswürdigen Maßstab für KI, LLM und überwachte Lernsysteme, insbesondere wenn sie über skalierbare Cloud-Analyse-Dienste oder moderne Datenplattformen implementiert wird.
Anwendungsbereiche
Die logistische Regression wird branchenübergreifend angewendet, um komplexe Daten in umsetzbare Erkenntnisse durch genaue Wahrscheinlichkeits- und Klassifikationsmodellierung umzuwandeln.
- Gesundheitswesen: Sie sagt die Wahrscheinlichkeit von Krankheiten wie Diabetes oder Herzkrankheiten unter Verwendung von Variablen wie Alter, Gewicht, Blutdruck und medizinischer Vorgeschichte voraus.
- Finanzen Sie hilft, die Chancen auf Kreditgenehmigung zu schätzen, betrügerische Transaktionen zu erkennen und das Investitionsrisiko zu bewerten, um Transparenz und Compliance zu gewährleisten.
- Marketing- und Kundenanalytik: Sie kann verwendet werden, um Kundenabwanderung oder Kaufabsicht aus Verhaltensdaten vorherzusagen, was gezieltere und effektivere Kampagnen ermöglicht.
- Personal Sie hilft, die Mitarbeiterfluktuation oder den Rekrutierungserfolg basierend auf den Merkmalen der Kandidaten und Leistungsindikatoren vorherzusagen.
- Fertigung und IoT: Sie kann verwendet werden, um Ausfälle von Geräten oder Produktionsprobleme durch überwacht Lernen auf Sensordaten vorherzusagen, was die prädiktive Wartung unterstützt.
- KI und Machine Learning: Sie kann als Basis-Klassifikationsmodell verwendet werden, um die Leistung fortgeschrittener linearer Modelle, LLM oder Deep-Learning-Algorithmen zu vergleichen.
- Cloud-Analytik und -Computing: Es kann verwendet werden, um große Datensätze in Cloud-Umgebungen zu analysieren, Hypothesen zu testen und Echtzeiteinblicke durch skalierbare logistische Modelle zu generieren.
Praktische Beispiele
1. E-Mail-Spam-Erkennung
E-Mail-Systeme verwenden logistische Regressionsmodelle, um Nachrichten als Spam oder legitim zu klassifizieren. Durch die Analyse von Merkmalen wie dem Verhalten des Absenders, Textmustern und Anhangstypen schätzt das Modell die Wahrscheinlichkeit, dass eine Nachricht zur Spam-Klasse gehört. Groß angelegte Datensätze ermöglichen eine genaue Klassifizierung durch effiziente maschinelle Lernpipelines.
2. Medizinische Diagnose
Im Gesundheitswesen sagt die logistische Regression die Wahrscheinlichkeit einer Krankheit basierend auf unabhängigen Variablen wie Alter, Blutdruck oder Glukosespiegel voraus. Integriert in prädiktive Analytik und maschinelle Lernsysteme hilft sie Klinikern, Risiken zu bewerten und informierte, datengestützte Entscheidungen zu treffen.
3. Kundenabwanderungsvorhersage
Unternehmen verlassen sich auf logistische Regression, um vorherzusagen, ob ein Kunde loyal bleibt oder abwandert, basierend auf Variablen wie Kaufhäufigkeit, Engagement oder Zufriedenheitswerten. Das Modell identifiziert die einflussreichsten Merkmale und hilft Teams, bevor die Abwanderung eintritt, zu handeln.
4 Kreditbewertung im Finanzwesen
Finanzinstitute verlassen sich auf logistische Regression, um die Wahrscheinlichkeit eines Kreditausfalls anhand historischer Daten zu berechnen. Durch die Analyse des Verhaltens von Antragstellern und finanzieller Muster können Banken beispielsweise erklärbare Vorhersagen für Risikobewertung und Compliance nutzen.
5 Systemleistung und Zuverlässigkeit
In einer Cloud-Architektur sagt die logistische Regression potenzielle Systemausfälle oder -verlangsamungen voraus. Die Überwachung mehrerer Variablen ermöglicht es Ingenieuren, die Wahrscheinlichkeit eines Ausfalls abzuschätzen und präventiv zu handeln, um Stabilität in groß angelegten Umgebungen zu gewährleisten.
Implementierung der logistischen Regression
Die Implementierung der logistischen Regression umfasst eine Reihe klarer Schritte, von der Datenvorbereitung bis zur Bewertung, wie gut das Modell reale Ergebnisse vorhersagt. Moderne Cloud-Computing- und Datenplattformen machen diese Prozesse skalierbar und effizient, selbst für große und komplexe Datensätze.
Der Prozess beginnt mit der Datensammlung und -vorverarbeitung. Analysten identifizieren relevante unabhängige Variablen, bereinigen die Proben und teilen sie in Trainings- und Testdatensätze auf – ein entscheidender Schritt im überwachten Lernen. Während des Trainings werden die Parameter (einschließlich des Schnittpunkts und der Koeffizienten) mit Optimierungsmethoden wie dem Gradientenabstieg verfeinert, um die Verlustfunktion zu minimieren und die Anpassung zu verbessern.
Nach dem Training stellen Validierungstechniken wie die Likelihood-Analyse oder Kreuzvalidierung sicher, dass das Modell gut generalisiert. Häufige Metriken wie Präzision, Recall, F1-Score und ROC-AUC bewerten, wie effektiv das logistische Modell in der Praxis funktioniert.
In Kombination mit einer skalierbaren Infrastruktur wird die logistische Regression zu einer leistungsstarken Grundlage für KI-, LLM- und prädiktive Analytikanwendungen.
Annahmen und Einschränkungen der logistischen Regression
Wichtige Annahmen
Während die logistische Regression anpassungsfähig ist, müssen mehrere wichtige Annahmen zutreffen, um genaue Vorhersagen und zuverlässige Analysen zu gewährleisten:
1. Binäre oder kategoriale abhängige Variable
Die abhängige Variable sollte binär (zwei Ergebnisse) oder kategorial (für multinomiale Regression) sein. Dies ermöglicht es dem Modell, Wahrscheinlichkeiten zu schätzen und jede Probe der richtigen Klasse zuzuordnen.
2. Lineare Beziehung mit dem Logit
Die logistische Regression geht von einer linearen Beziehung zwischen Prädiktoren und dem Logit – dem Logarithmus der Quoten – aus. Analysten überprüfen dies, indem sie Residuenplots untersuchen oder Variablen transformieren, um die Anpassung zu verbessern.
3. Unabhängigkeit der Beobachtungen
Jede Beobachtung muss unabhängig sein. Wiederholte oder korrelierte Proben können Parameter verzerren und Wahrscheinlichkeitsabschätzungen verfälschen.
4 Abwesenheit von Multikollinearität
Unabhängige Variablen sollten nicht hoch korreliert sein. Werkzeuge wie der Varianz-Inflationsfaktor (VIF) helfen, Multikollinearität zu erkennen, was stabile Parameterschätzungen und eine klarere Merkmalsinterpretation gewährleistet.
5 Ausreichende Stichprobengröße
Ein großes Datenset erhöht die Zuverlässigkeit, indem es zufällige Variationen in der Verlustfunktion reduziert und die Präzision der geschätzten Werte und Parameter verbessert.
Beschränkungen
Trotz seiner Vielseitigkeit hat die logistische Regression einige praktische Einschränkungen, die Analysten bei der Erstellung von Klassifikationsmodellen berücksichtigen sollten:
1. Linearität im Logit
Obwohl flexibler als die lineare Regression, geht sie immer noch von einer linearen Beziehung zwischen Prädiktor und Logit aus. Nicht-lineare Interaktionen können Feature Engineering oder polynomiale Variablen erfordern, um die Anpassung zu verbessern.
2. Umgang mit mehreren Klassen
Die Standard-logistische Regression eignet sich am besten für binäre Ergebnisse. Während multinomiale Modelle mehr Klassen verarbeiten können, erhöhen sie die rechnerische Komplexität und erfordern oft größere Datensätze für Genauigkeit.
3. Empfindlichkeit gegenüber Ausreißern
Ausreißer können Parameter und Wahrscheinlichkeitsabschätzungen verzerren. Die Normalisierung oder Transformation von Werten vor dem Training hilft, das Modell zu stabilisieren und die Zuverlässigkeit zu verbessern.
4 Datenabhängigkeit
Die Genauigkeit eines logistischen Modells hängt stark von sauberen, ausgewogenen Daten ab. Geräuschhafte oder verzerrte Proben können die Vorhersageleistung verringern, was die Datenvorbereitung unerlässlich macht.
5 Rechnerische Skalierbarkeit
Obwohl leichter als Deep Learning, erfordert die großangelegte logistische Regression dennoch erhebliche Rechenleistung. Dies führt oft zu dem Bedarf an einer skalierbaren Cloud-Infrastruktur, die Ressourcen effizient erweitern kann, während sie eine konsistente Leistung und Modellgenauigkeit aufrechterhält.
Interpretation der Ergebnisse der logistischen Regression
Sobald ein logistische Regressionsmodell trainiert wurde, besteht der nächste Schritt darin, die Ergebnisse zu interpretieren. Dieser Prozess verwandelt mathematische Parameter in bedeutungsvolle Erkenntnisse und hilft Analysten zu verstehen, wie jede Variable die Wahrscheinlichkeit eines Ergebnisses beeinflusst. Eine ordnungsgemäße Interpretation stellt sicher, dass die Analyse genau, umsetzbar und relevant für die Entscheidungsfindung in der realen Welt ist, egal ob lokal oder über Cloud-Analyse-Dienste durchgeführt.
Verständnis der Ausgab Zusammenfassung
Die Ausgabe eines logistischen Regressionsmodells umfasst typischerweise mehrere wichtige Komponenten, die erklären, wie das Modell die Daten anpasst und wie man seine Vorhersagen interpretiert:
1. Koeffizienten (Parameter)
Jeder Koeffizient misst den Einfluss einer erklärenden Variablen auf die Chancen eines bestimmten Ergebnisses. Ein positiver Wert erhöht die Wahrscheinlichkeit des Eintretens des Ereignisses, und ein negativer Wert verringert sie. Die Exponentiation dieser Koeffizienten ergibt Odds Ratios, die die Ergebnisse leichter interpretierbar und vergleichbar machen.
2. Achse (Konstanten)
Die Achse repräsentiert die Basis-Log-Odds des Ereignisses, wenn alle unabhängigen Variablen auf null gesetzt sind. Sie dient als Referenzpunkt, von dem aus alle anderen Effekte gemessen werden.
3. P-Werte und Signifikanz
P-Werte bestimmen, welche Variablen signifikant zum Modell beitragen. Ein p-Wert unter 0,05 zeigt im Allgemeinen an, dass das Merkmal einen bedeutenden Einfluss auf das Ergebnis hat, was Analysten hilft, die Modellanpassung zu verfeinern und irrelevante Prädiktoren zu entfernen.
4 Modellanpassungsmetriken
Häufige Metriken wie Log-Likelihood, AIC (Akaike-Informationskriterium) und pseudo-R² bewerten, wie gut das Modell die beobachteten Daten erklärt. Diese helfen zu bestimmen, ob die aktuelle Menge an Variablen optimal ist oder ob weitere Anpassungen erforderlich sind, um den Verlust zu reduzieren.
5 Konfusionsmatrix und Leistungskennzahlen
Die Konfusionsmatrix vergleicht vorhergesagte und tatsächliche Ergebnisse und gibt ein klares Bild der Klassifikationsgenauigkeit. Komplementäre Metriken wie Präzision, Rückruf, F1-Score und ROC-AUC fassen zusammen, wie effektiv das logistische Modell zwischen Klassen unterscheidet.
Validierung logistischer Regressionsmodelle
Die Validierung stellt sicher, dass ein logistisches Regressionsmodell zuverlässig mit unbekannten Daten funktioniert – nicht nur mit dem Trainingssatz. Es ist ein kritischer Schritt zur Bestätigung der Genauigkeit und zur Vermeidung von Überanpassung. Häufige Validierungstechniken sind:
- Kreuzvalidierung: Das Aufteilen des Datensatzes in Falten, um die Robustheit des Modells zu testen und zufällige Verzerrungen zu reduzieren.
- Bootstrapping: Zufälliges Resampling der Daten, um die Stabilität der Parameter und Vorhersagewerte zu schätzen.
- Holdout-Tests: Einen Teil der Daten ausschließlich für die endgültige Bewertung nach dem Training reservieren, um eine echte Leistungsbewertung sicherzustellen.
Durch die Kombination dieser Methoden können Analysten beurteilen, ob das Modell effektiv auf neue Proben generalisiert. Zuverlässige Validierung bestätigt nicht nur die Vorhersagegenauigkeit, sondern verbessert auch das Vertrauen bei der Bereitstellung logistischer Regression in realen KI-, LLM- oder prädiktiven Analyseanwendungen.
OVHcloud-Lösungen für logistische Regression
OVHcloud bietet eine Reihe von Cloud-Produkten an, die Ihnen helfen, logistische Regression und andere ML-Modelle effizient zu erstellen, zu trainieren und zu skalieren. Von Rechenleistung über sichere Speicherung bis hin zur KI-Bereitstellung unterstützt jede Lösung datengestützte Innovationen in großem Maßstab:

Public Cloud
Führen Sie logistische Modelle mühelos in einer flexiblen, nutzungsabhängigen Umgebung aus und skalieren Sie diese. Die Public Cloud bietet virtuelle Maschinen, Blockspeicher und Lastenausgleich für leistungsstarke Datenanalysen und prädiktive Analytik-Workloads. Perfekt für die Verarbeitung großer Datensätze, das Testen mehrerer Modelle oder die Integration von überwachten Lernpipelines.

Dedicated Server
Für rechenintensive Klassifikations- oder multinomiale Regressionsprojekte bieten dedizierte Server rohe Leistung und volle Kontrolle. Diese Bare-Metal-Lösungen sind ideal für die Verarbeitung großer Datenmengen, das Ausführen fortschrittlicher KI-Workloads oder das gleichzeitige Trainieren mehrerer logistischer Regressionsmodelle, mit vorhersehbaren Preisen und hoher Verfügbarkeit.

KI- und ML-Lösungen
Trainieren, optimieren und implementieren Sie Ihre logistischen Regressions- und Machine-Learning-Workflows mit AI Training und AI Deploy. Diese verwalteten PaaS-Plattformen vereinfachen das überwachte Lernen und ermöglichen nahtlose Übergänge von Experimenten zur Produktion, alles in einer sicheren, skalierbaren Cloud-Umgebung.

Data Platform und Speicher
Speichern, verwalten und analysieren Sie Ihre Daten effizient mit der Data Platform und Objektspeicher. Diese Dienste bilden die Grundlage für den Aufbau von Datenpipelines und unterstützen Echtzeit-Modellaktualisierungen sowie langfristige prädiktive Analytikprojekte.